Pourquoi ce modèle?
Ce petit modèle a été conçu par Jacques Desrousseaux (1910-1993) à l'attention de ses enfants. D'un abord mathématique simple, du niveau terminal, il constitue une introduction à la science économique en général et aux ouvrages un peu plus complexes écrits et publiés au cours de sa vie professionnelle, dont nous avons dressé la liste ci-dessous.
Il aurait approuvé que nous en fassions profiter ceux qui s'intéressent à la science économique, science étant pris au sens propre du terme. C'est pourquoi nous le publions sur ce site. La copie est libre de droits. La seule chose que nous, sa femme et ses enfants, demandons à ceux qui y trouvent quelque intérêt, c'est de ne le diffuser qu'avec les références à l'auteur et de ne pas le modifier sans notre autorisation.
La prise de contact avec le rédacteur du site peut se faire par l'email joint.
Oeuvres de Jacques Desrousseaux
1- Bassins houillers et lignitifères de la France. Mémoires annexes de la statistique de l'industrie minérale, 1938.
2- Caractéristiques des économies quelconques et taux d'intérêt optimal dans les mondes évolutifs. Séminaire Allais (GRES), 25 mai 1961.
3- L'évolution économique et le comportement industriel. Dunod, Finance et Economie appliquée, nº19, 1965.
4- La stratégie de l'entreprise. La Pensée Universelle, 1978.
5- Théorie des ressources naturelles non renouvelables. Monographies du séminaire d'économétrie du CNRS. Nº22, 1980.
6- La théorie économique et l'espace géographique. Monographies du séminaire d'économétrie du CNRS. Nº17, 1981.
But
Introduction aux méthodes économiques et définition des termes, ceci sur un modèle simple et discontinu (divisé en années).
Remarques et conventions d'écriture
Les notations, y compris les formules, sont en mode texte. Lorsqu'elles sont un peu compliquées, elles sont transcrites de façon conventionnelle.
Les sommes se notent :
s[a :b]f (n), pour les fonctions discrètes de nombres entiers,
s[a :b]f (x)dx, pour les intégrales.
d se lit d rond :d°Q/d°x, drond Q sur drond x.
Les variables des formules du type {Np=No* (1+a) } sont discontinues. Les graphes images seront cependant tracés en mode continu, sous la forme :
y=No (1+a)^x, ou
y= No*exp (ln (1+a)), ce qui est identique.
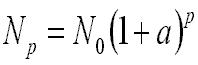
Dans le graphe {01}, les paliers représentent la fonction discrète, et la courbe, la fonction continue.
I - Données
On étudie la vie d'un village d'artisans spécialisés. Ce village rassemble {Np} actifs l'année {p}, et leur taux de croissance est {a}, c'est-à-dire que :
{01} : {Np=No* ( (I+a))}, soit
Le bien produit par ces artisans est consommé par le village, une partie étant troquée à l'extérieur (ou vendue) pour permettre l'acquisition d'autres biens de consommation (le Taux de troc est supposé constant dans le temps). Si la quantité produite est {Qp}, on appelle "niveau de vie" la notion physique :
{02} : {V=Qp/Np}, soit
Autrefois les artisans travaillaient à la main. Il fallait 22 personnes pour produire Q=10 unités de bien ci-dessus.
Aujourd'hui, les artisans savent faire une machine donnant la production {1} ; pour cela, le patron artisan de l'atelier (qui travaille avec ses compagnons) a besoin de {x} personnes travaillant pendant un an ; puis la machine faite, elle dure un an avant d'être hors d'usage ; elle produit alors, l'année après sa construction, une unité du bien, ceci en utilisant le travail de {y} artisans. On appelle "capitalistiques" ces procédés exigeant un matériel construit avant que l'on ne puisse produire (ce matériel est un "bien de capital", dont la valeur en monnaie est le "capital" du patron propriétaire).
I. a - Emprunts
Pendant l'investissement (fabrication du bien de capital), le patron doit payer son personnel (et vivre lui-même). Pour cela il emprunte de l'argent (à l'extérieur ou à l'intérieur du village), au taux d'intérêt {i} du marché, qu'on suppose constant. Il remboursera l'emprunt l'année suivante, quand la machine produira.
I. b - Salaires
Dans le village, comme à l'extérieur, le salaire des travailleurs croît au taux {s}. Le "salaire nominal" est ainsi multiplié l'année {p} par
{04} : { (1+s)}.
Mais si la technique de production ne se perfectionne pas (nb : Progrès technique), il ne permet pas d'acquérir plus de biens, donc le "salaire réel" reste constant. Nous le supposerons ci-après.
II - Modèles
Le schéma précédent est un "modèle". Un modèle isole et simplifie certains mécanismes économiques, sans déformation des réflexes normaux des agents économiques. Le but est de comprendre qualitativement et si possible quantitativement les effets des "commandes" mises en œuvre par ces agents (décisions économique de tous ordres ; achats, ventes, investissements, emprunts, travail)
Si la théorie générale est exacte, les écarts entre ses résultats et ceux des modèles doivent être expliqués ; il peut s'agir d'erreurs de la théorie générale, et c'est alors une source de découvertes scientifiques ; elles peuvent aussi tenir à la simplification exagérée des modèles, à l'insuffisance du nombre de commandes libres ou à des contraintes entachées d'incompatibilités internes.
Dans le modèle ci-dessus, il n'y a qu'une commande de l'économie, savoir le choix de la technique utilisée. Pour le reste, les ouvriers doivent bien tous travailler, et les patrons emprunter pour investir ; la société est égalitaire, le bien {Q} étant également réparti entre tous (avec des salaires égaux) ; le modèle ne peut donc déceler aucun effet du chômage éventuel, ou des inégalités de "répartition des revenus" que présente le monde réel. Or, l'ouvrier travaille ou ne travaille pas, quitte ou non le village, chaque investissement fait l'objet de décisions autonomes et spécifiques, les prêteurs ont ou n'ont pas envie de prêter à tel taux etc. Mais le modèle n'apprendra rien d'autre que les effets du choix de la technique capitalistique d'une part, de l'écoulement du temps d'autre part. De nombreux modèles et théories négligent le "facteur temps" et conduisent à des résultats très erronés, ce qui risque de marquer gravement et parfois définitivement les étudiants. Certaines connaissances intertemporelles permettent de parer à cet inconvénient grave, le présent modèle permet d'entrer d'emblée dans le réel sous cet angle.
Ainsi, chaque modèle ne peut donner que des résultats très partiels, limités à l'effet des "commandes" qu'il retient, et encore si les contraintes retenues ne limitent pas plus que de n'est le cas en réalité les effets de ces commandes.
III - Intérêt et actualisation
Pour obtenir un prêt financier, il faut payer un intérêt au taux {i}. Notre patron artisan doit trouver de quoi payer l'année {0} ses {x} ouvriers utilisés pendant la période d'investissement, en remboursant l'année d'après, où il vendra la production. Si l'unité de valeur est le salaire de l'année {0}, l'emprunt à contacter est de {x}, et le patron devra payer l'année suivante {x*i} d'intérêts et {x} de remboursement, soit au total total :
{05} :{x* (1+i)}.
S'il devait attendre deux ans pour produire, il devrait réemprunter {x* (1+i)} l'année un, pour verser, sur les recettes de l'année deux, et ainsi de suite, soit {x* (1+i)} pour l'année {p}.
On vérifie que le résultat ne dépend pas des modalités d'emprunt. Par exemple, si j'emprunte {x} l'année {0}, verse les intérêts {i*x} les années {un} et {deux}, et rembourse l'année deux, j'ai dû emprunter {i*x} l'année un, d'où une échéance {i*x* (1+x)} l'année {deux}. Finalement, mes {x} m'ont coûté l'année deux un total de {x+i*x+i*x (1+ix)}={x* (1+i)^2}. Tout ceci est également vrai dans l'autre sens (fonds prêtés).
En conclusion, dans un monde où l'intérêt est {i}, il y a équivalence de fait entre les sommes : {xo}, {xi=xo* (1+i)}, {x2=xo* (1+i)^2},, {xp}={xo* (1+i)}… des années {O}, {1},,{p}
Si donc je dépense les sommes {So}, {S1}, {S2},,{Sp} les années {0} à {p}, tout se passe pour moi comme si je dépensais l'année zéro :
{06} : {S=So+S1/ (i+i)+S2/ ( (1+i)^2)+…+Sp/ ( (1+i))}, soit
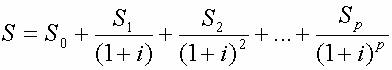
Ce total est appelé "valeur actualisée" à l'époque des débours des années zéro à p. Le "cœfficient d'actualisation" est (i}. Ici, il coïncide avec le taux d'intérêt du marché financier, mais il faut s'habituer à distinguer l'un de l'autre, car dans les problèmes plus complexes, il peut y avoir césure entre le taux d'intérêt, données financières, et le taux d'actualisation, qui peut être afférent à d'autres types d'équivalences entre époques que l'équivalence pour le porte-monnaie.
III. a - Application au modèle
La production unitaire de l'année +1 coûte au patron artisan
- l'année zéro {x} unité de salaire ;
- l'année un y unités de salaire de l'époque un, soit {y* (1+S)}
Soit un coût, actualisé à l'époque zéro, de
{x+y* (1+s)/ (1+i)}
Le "coût du produit" fabriqué l'année un comporte :
{y* (1+s}) versés cette année,
{x* (1+i}), valeur actualisée des salaires versés l'année zéro, et qu'il faut verser l'année un aux prêteurs qui ont permis l'investissement.
D'où le coût total unitaire :
{07} : {C=y* (1+s)+x* (1+i)}, soit
C'est à ce coût que sera fixé le prix de vente du produit, pour pouvoir juste couvrir les salaires (uniformes) des travailleurs et du patron-artisan.
IV - Monnaie effective et monnaie de compte
La monnaie effective, d'après l'énoncée, comporte accroissement de salaire au taux "s". Mais elle ne permet pas l'accroissement du niveau de vie, puisqu'on ne peut consommer plus qu'on a produit.
Il est commode de faire les calculs économiques dans une autre unité appelée "monnaie de compte" et qui soit "stable". Ici, elle sera telle que le salaire soit constant, ce qui stabilisera le prix du bien produit. S'il y a progrès technique [nb : Progrès technique], alors on peut prendre la "monnaie salariale" telle que le salaire soit constant {s=0} et le prix du produit en baisse (au taux c), ou encore la monnaie à base réelle (ne pas confondre avec la monnaie effective) telle que le prix du produit soit stable, mais alors les salaires croissent au taux {c}. Ceci montre la relativité de la notion de monnaie stable.
L'économiste doit savoir manipuler toutes les unités monétaires alternatives. Les ménagères françaises savaient le faire il y a peu de siècles, quand la monnaie nationale effective, trop instable, ne servait pas à la fixation des prix. Les marchands étiquetaient les prix en monnaie de compte stable, que l'on payait en écus plus ou moins rognés "effectifs" selon le taux de change affiché chaque jour.
Le passage d'une monnaie à une autre toutes choses égales d'ailleurs du côté de l'économie "physique" exige des changements de taux de croissance. Ainsi, si le salaire est {x* ( (1+s))} à l'époque {p}, et si le progrès technique est au taux {c} - ce qui permet un accroissement au même taux des accroissements par tête, alors le salaire en monnaie de compte à base réelle varie comme { (1+c)}. Tous les prix, coûts, salaires du système effectif, pour passer à la monnaie de compte sont à multiplier par :
{08} : {w= ( ((1+c)/ (1+s)))} voisin de {1+c-s}, soit :
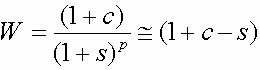
On calcule donc les nouveaux taux par des différences ou additions des anciens. Ce procédé semble approximatif, mais il est en réalité rigoureux dans le monde continu et non discontinu qu'est le monde réel. Il suffit en effet de remplaçer a par {a1=ln (1+a)} et {p} par l'époque {t} ; en continu {s} devient {exp (s1*t)} et {w} devient {exp (c1-s1)*t} très exactement. Le taux résultant est bien {c1-s1} exactement. Le remplacement des modèles discontinus par des modèles à temps continu donne souvent une bien plus grande puissance aux études, mais il ne faut le faire que quand on est très familiarisé avec les méthodes économiques.
IV. a - Taux d'actualisation et taux d'intêrêt
Qu'en est-il de ces deux taux dans les passages aux monnaies de compte ? Pour une structure physique identique de l'économie -celle que l'on étudie- et si l'on prend une monnaie de compte distincte de la monnaie réelle, il faut adapter le taux d'intérêt. L'identité physique implique en effet des choix identiques des individus ; si ces choix portent sur deux époques distinctes, les termes en balance doivent être identiques.
Pour le prêteur, qui opte entre garder la somme So dont il dispose, ou la prêter et retrouver {so* (1+i)} dans un an, le premier terme du choix est le même, mais le second, savoir l'utilisation réelle qu'il fera de ses fonds, exige pour être identique que la somme récupérée l'année un passe à
{} {So* (1+i) (1+d)}
Si les prix de la monnaie de compte croissent au taux {d} par rapport aux prix initiaux ; et si le nouveau taux d'intérêt est {j}, on doit avoir :
{} : {{1+j= (1+i)* (1+d)}.
De même, le producteur qui fait des choix techniques entre les dépenses de travail ou de fournitures, ou des quantités produites de deux années ultérieures distantes de {p} années, ce producteur ne fera les mêmes choix que si les cœfficients d'actualisation nouveaux compensent les modifications de prix et conduisent aux mêmes termes d'échange sur la base des prix d'une même époque ; ceci donne :
{} {1/ ( (1+i))= ( (1+d))/ ( (1+j))}
soit encore
{} {1+j= (1+i)* (1+d)}
Ainsi on doit prendre comme nouveau taux d'intérêt (et d'actualisation) (j) tel que
{} : {j-d=i}
(sensiblement en discontinu, exactement en continu, comme indiqué à l'alinéa précédent le §4a). Si {i} est le taux dans une monnaie "stable" (à définir plus précisément, voir au début du §4), on a coutume d'appeler {j-d}, différence du taux et de la revalorisation relative des monnaies, "taux d'intérêt réel" ; on peut alors dire qu'une monnaie est "neutre", (c'est-à-dire ne conduit à aucune modification d'évolution économique) si le taux d'intérêt réel y est maintenu égal à celui de la monnaie de base stable (ou, si l'on veut s'il y a égalité du taux réel de la monnaie effective et de la monnaie de compte). Le taux d'actualisation jouit de la même propriété, bien entendu ici parce qu'il égale le taux d'intérêt, mais même dans le cas le plus général.
V - Fonction de production
Pour simplifier les calculs, utilisons tout de suite les résultats du §4. Prenons la monnaie de compte "salariale", soit s=0, ce qui impose pour le maintien du système physique un certain taux d'intérêt {i}, égal au nominal dans le système {s}, diminué de {s}.
La quantité produite par la meilleure technique du moment dépend des facteurs de production utilisés, qui sont ici {x} et {y}, travaux fournis lors de l'investissement et pour l'exploitation ultérieure. On peut utiliser des procédés plus ou moins "capitalistiques", c'est-à-dire conduisant à des rapports {x/y} plus ou moins élevés.
La fonction de production est la relation
{} : {Q=Q (x, y)},
qui donne la production en fonction des quantités de facteurs qu'elle consomme. Le patron-artisan choisit bien entendu le procédé occasionnant le minimum de coût actualisé pour une production donnée, soit :
- production donnée,
{09a} : { (d°Q/d°x)*dx+ (d°Q/d°y)*dy=0} ;
- coût minimal,
{09b} : { (1+i)*dx+dy=0},
soit in fine,
{09c} : { (d°Q/d°x)= (d°Q/d°y)* (1+i)}
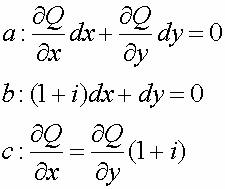
qui donne, avec Q=Q (x, y),
{} : x (Q) et y (Q).
Nous supposerons ici qu'on ne sait faire que des machines unitaires {Q=1}, et que pour ces machines, {x*y=1}. D'où la technique choisie
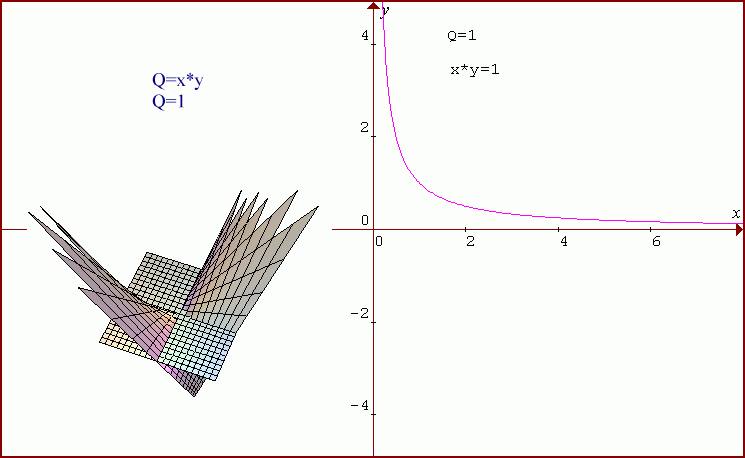
{10a} {y=x* (1+i)} soit :
{10b} : {x=1/rac (1+i)}
{10c} : {y=rac (1+i)}
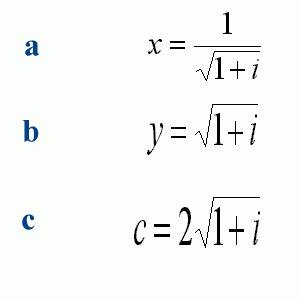
Le coût unitaire, auquel on devra vendre le produit, sera alors {§3a} :
{10d} : {C=2*rac (1+i)}.
V. a - Fonction de production homogène
On dit que da fonction jouit de l'homogénéité quand la production est multipliée par {k} quand tous les facteurs {y} intevenant sont multipliés par {k}. C'est le cas avec les machines unitaires, et la fonction de production (homogène) s'écrit :
{11} : {Q=rac (x*y)}
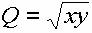
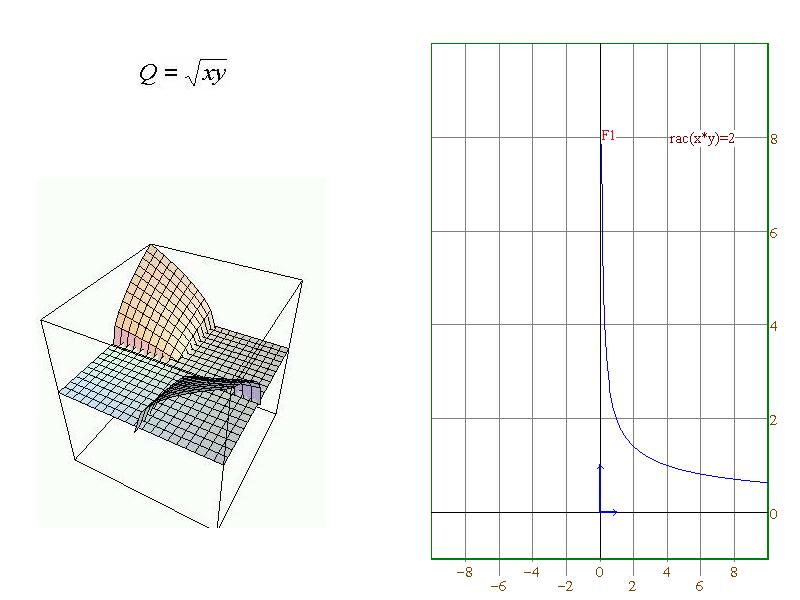
V. b - Non homogénéité, coût marginal
Dans le cas contraire, il y a "effet d'échelle" et le coût dépend de l'échelle de la production. Dans l'industrie, le "rendement croissant" est la règle ; plus on produit, plus chaque facteur est efficace. L'effet d'échelle est alors une réduction du coût avec la production, et l'existence d'un coût marginal inférieur au coût moyen. Si par exemple, {Q=x*y}, l'optimum donne toujours {y=x* (1+i)}, mais il vient :
{12a} : {x=rac (Q)/rac (1+i)}
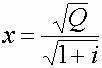
{12b} : {y=rac (Q)*rac (1+i)}
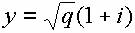
Le coût moyen est
{12c} : {C/Q=2*rac (1+i)/rac (Q)},
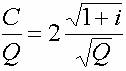
et le coût de l'unité en plus ou "coût marginal", {dC/dQ} s'établit à
{12d} : {rac (1+i)/rac (Q)},
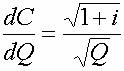
soit la moitié du coût moyen {C/Q}. Ce sont là des ordres de grandeur très courants dans les industries modernes.
Pour en terminer avec les choix des producteurs, voyons l'intérêt du processus capitalistique par rapport au processus direct qui, on l'a dit au début, exigeait 22 artisans pour une production {Q=10}. On a vu que le coût du système moderne était, pour une production unitaire, {C=2*rac (1+i)}. Le système primitif coûtant 2. 2, dans la même unité salariale, il ne redeviendrait intéressant que si le taux {i}, intérêt réel, donc toujours assez faible, excédait { ( (1. 1)^2)-1= 21%}. C'est hors de la plaque (c'est-à-dire improbable dans le monde réel).
VI - Évolution du niveau de vie
La production de l'année {p}, soit {Q (p)}, est assurée par {y*Q (p)} artisans. Le reste de la population active s'occupe à fabriquer des machines pour la période de production {p+1}, soit {x*Q (p+1)}. Le total étant {N (p)}, on a :
{} : {y*Q (p)+x*Q (p+1)=N (p)}
Posons {1+i=u} et {1+a=v} et remplaçons x, y et N (p) par leur valeur du {10a, 10c}, savoir {u^ (-1/2)},{u^ (1/2)} et {No * (v^p)}, il vient alors :
{13} : {u*Q (p)+Q (p+1)=No* (v)*u^ (1/2)}
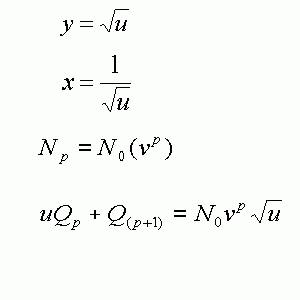
VI. a - Régime exponentiel permanent
Cherchons s'il existe un régime où tous les paramètres restent les mêmes au cœfficient {v} près. Il vient :
{14} : u*Q (p)+v*Q (p)=N (p)*rac (u^ (1/2))
(v) est donné ; cherchons l'optimum du niveau de vie (V). dv/du=0 donne v=u, soit i=a. Ce résultat est absolument général ; dans un régime exponentiel permanent, il existe un taux d'intérêt optimal qui, en monnaie quelconque, égale le taux de progression nominal des salaires totaux (ce dernier taux additionne la croissance du nombre de travailleurs actifs, la croissance de leur salaire réel et le taux de dévalorisation monétaire (théorème du taux d'intérêt optimal).
A une époque donnée, la fraction {y/N} des travailleurs, soit {u/ (u+v)}, est employée dans les industries de consommation, le reste {v/ (u+v)} dans les fabrications de biens d'investissement. A l'optimum (v=u), le partage est égal.
VI. b - Régimes quelconques
Dans les faits, la situation initiale nous échappe, nous héritons à l'époque zéro de ce qui existe comme investissements. Ici, ce capital physique initial est l'outil de capacité {Qo}.
Comment variera le niveau de vie Vp quand on part de ce capital Qo (ou si l'on veut, du niveau de vie initial Vo) ?
La suite des relations du début du §6 nous donne par récurrence :
{15a} : {Vp=Vr+ (-1)* ( (u/v)) (Vo-Vr)},
soit en continu :
{15b} : {V (t)=V (r)+ (v (0)-v (r))cos (pi*t)*exp (t*ln (u/v)}
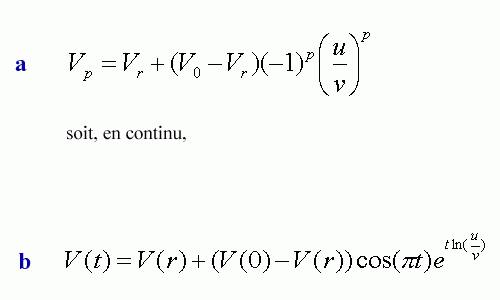
relation où V est le niveau de vie du système de référence de type exponentiel permanent du §6. a, soit {Vr= rac (u)/ (u+v)}. Comme on le voit, l'écart initial {Vo-Vr} provoque des fluctuations ultérieures, Vp passant successivement en dessus et en dessous de la constante {Vr} (ou vice versa).
- Précautions d'usage des modèles
On voit que si {u inférieur à v}, c'est-à-dire {i inférieur à a}, les oscillations s'amortissent et l'on tend vers le régime de référence. Sinon, il y a divergence et même blocage à partir d'un certain moment (en fait, impossibilité d'utiliser à certaines époques les équipements fabriqués l'année précédente). Ce fait est particulier au modèle, que sa commande unique rend trop rigide pour les adaptations nécessaires ; il disparaît sur les modèles plus complexes, mais qui sont très difficiles à monter et à comprendre.
Cet incident montre qu'il faut conserver aux "petits modèles" un rôle limité et ne pas croire qu'ils suffisent à démontrer la théorie économique générale. Leur usage licite est double :
- permettre de comprendre les conclusions de la théorie générale, que sa grande complication rend très ésotérique,
- déceler des anomalies que l'on étudiera alors sur le plan général, pour chercher si la théorie ne doit pas être amendée.
Ce dernier cas ne se présente pas ici. En portant le problème des taux d'intérêt élevés au niveau général, on constate que cette anomalie n'existe pas, mais on en trouve une autre qui n'apparaît pas ici où l'on n'étudie pas la répartition entre travailleurs et capitalistes.
- un blocage effectif se produit bien parfois, qui se résume au paradoxe classique du sou placé à l'époque de Jésus-Christ, à intérêts composés, et dont le titulaire possède aujourd'hui de loin plus que la totalité du globe. Si les prêteurs de l'argent nécessaire aux investissements (capitalistes) sont "purs" et replacent leur mise ainsi que leurs intérêts, leur capital croît plus vite que la richesse de la nation si i}a. Les placements deviennent impossibles. Le blocage se résoud naturellement de lui-même par un changement d'attitude des capitalistes, notammment une baisse des taux d'intérêt.
Ceci est caractéristique des précautions nécessaires en économie.
Finalement, la répartition des niveaux de vie dans le temps, s'établit selon un système de courbes du genre de celles du graphique annexe (où l'on est revenu à la réalité continue, et où l'année est remplacée par lz durée de vie des machines).
Les gouvernements disposent de moyens d'action puissants pour passer d'une courbe à l'autre :
- ils peuvent prendre des mesures temporaires pour passer d'un niveau initial Vo à un autre, par exemple Vr, dans le but de stabiliser l'évolution,
- ils peuvent aussi préférer une courbe du type {I}, par exemple s'il y a des élections l'année 2 ;
- ils savent aussi agir sur le taux d'intérêt à long terme, qui ne résulte plus guère de l'offre et de la demande de capitaux, mais bien de la politique monétaire et financière de l'état et d'un appareil bancaire qu'il contrôle de plus en plus directement. On peut alors modifier l'état de référence Vr.
Ce qui est important et contraire à la "théorie concurrentielle classique", c'est que certaines évolutions sont en permanence plus avantageuses que certaines autres qui, cependant, répondent tout autant aux critères classiques (lesquels admettent tous les taux d'intérêt que peuvent fixer l'offre et la demande de capitaux).
En fin de compte, on voit que le taux d'intérêt (ou plutôt le taux d'actualisation servant aux calculs des industriels) a un effet sur la répartition dans le temps des niveaux de vie, et même sur leur niveau absolu, effet que des modèles plus complexes montrent être considérables. A politique d'évolution intertemporelle donnée correspond une suite précise de taux d'actualisation. L'ennui est que l'on ne sait guère la calculer, pour le moment ; les tentatives du Plan restent à cet égard très discutables.
VII - Optimum Pareto
Il s'agit maintenant du "petit cours supérieur".
L'optimum Pareto, utilisé par les théories classiques, s'intéresse aux seules "satisfactions" procurées aux individus par les biens de consommation qu'ils acquièrent. Il signifie qu'aucune mesure de gestion n'aurait permis d'accroître les "satisfactions" d'un individu sans réduire celles d'un autre.
VII. a - Théorie classique
La théorie dite "concurrentielle classique" montre que si chaque producteur minimise son coût de revient et vend au coût marginal ; et si chaque acheteur d'un bien le choisit librement et selon son intérêt, alors on obtient l'optimum Pareto.
Elle prétend démontrer aussi bien d'autres résultats, dont nous n'avons pas besoin ici, et dont beaucoup sont faux, alors que l'énoncé ci-dessus est correct dans certaines conditions.
VII-b - Application aux époques distinctes
La théorie prétend appliquer son raisonnement aux époques futures ; si un homee, dit-elle, consent à prêter de l'argent à 5%, c'est qu'il préfère renoncer à un achat immédiat, pour se payer tel objet dans "n" années, avec le remboursement et les intérêts. Et s'il a envie tout de suite d'un bien plutôt que de l'acheter dans deux ans, il empruntera s'il le faut, et préfère agir ainsi que d'attendre, bien que dans deux ans, il doive constater qu'il a payé 110. 25 F. ce qu'il aurait maintenant pour 100 F. L'ennui c'est que les transferts d'argent dans le temps ne sont pratiqués que par très peu de personnes (sauf certains types de crédits, d'ailleurs à assez court terme et à taux très différent de celui du marché). Egalement que l'individu, quand il épargne, vise essentiellement une meilleure répartition des ses revenus pendant sa vie et non des achats particuliers. Autrefois, c'était ainsi qu'il constituait sa retraite, mais les incertitudes financières et économiques ont conduit à de tels désastres en la matière que tous les états ont bien dû en venir à d'autres méthodes pour assurer la sécurité sociale. L'effet du taux d'intérêt du marché, dit la théorie, est optimal puisque tous les achats se font à l'époque où la valeur subjective du bien est la plus satisfaisante pour l'intéressé, compte tenu du prix actualisé. Par malheur on ne trouve pas dans le même magasin l'objet d'aujourd'hui et celui de dans dix ans, et nul ne sait ce dont il aura absolument envie à cette époque, et quel en sera le prix ; l'hypothèse de "prévision parfaite" que fait la théorie, si elle est admissible pour la gestion d'une industrie, ne l'est absolument pas ici. En outre, si chacun connaît les effets des achats immédiats (les prix des oranges montent si tout le monde se jette dessus), il ignore totalement l'effet du taux d'intérêt sur l'évolutions des productions globales futures. Si l'on se reporte aux courbes de la page 6, on voit que si beaucoup de personnes se serrent la ceinture et placent leurs économies pour assurer leur avenir, la baisse résultant sur le marché du taux d'intérêt conduit à réduire les disponibilités futures en biens de consommation (si le taux est, comme d'habitude inférieur à "a"). C'est exactement le contraire de ce que désirent les intéressés. Donc la liberté du marché des capitaux n'a aucune raison de donner un optimum pour les satisfactions des acheteurs. La seule démarche efficace consiste donc en l'étude centrale des conséquences du taux d'intérêt, en un choix d'un taux ouvrant les meilleures perspectives, et en l'application des mesures voulues pour que les choix des industriels soient faits avec ce taux. Compte tenu de son contrôle sur les établissements financiers, l'État est tout à fait en mesure de mener cette politique, et il ne manque pas de le faire -sauf qu'il vise des objectifs à court terme et qui ne concernent que très indirectement les satisfactions des consommateurs (objectifs monétaires et financiers). Les tentatives faites par le Plan ne sont guère convaincantes ; il ne paraît pas qu'on soit capable de calculer sérieusement les effets économiques à long terme des taux d'intérêt, et il faudrait encore, en plus, que l'on accorde une priorité à ses objectifs sur ceux à court terme, ce qui n'est certes pas la tendance de la majorité des politiciens.
Si, dans ce domaine, la théorie est taxable d'irréalisme total, il faut ajouter qu'elle comporte en plus une erreur mathématique, que n'ont peut-être pas commise à la lettre les chercheurs qui l'ont établie, mais que commettent systématiquement ceux qui l'utilisent. On peut caractériser ainsi cette erreur : l'une des conditions mathématique de l'obtention de l'optimum Pareto (par les procédés indiqués au § 7), est l'existence de limites générales ; ces conditions sont évidemment remplies géographiquement (le globe est limité, on ne peut faire travailler plus d'hommes qu'il n'en existe ; on conçoit que des théories pour résorber le chômage doivent au contraire éliminer ces conditions aux limites, mais elles perdent toute validité dès que le chômage est éliminé, et la théorie générale est celle d'un long terme sans déséquilibres structurels durables). Mais l'intervention du temps modifie profondément la situation ; il y a bien une condition aux limites indiscutables, savoir l'état initial sur lequel on ne peut naturellement pas agir ; mais il n'y a pas de condition aux limites finales. On ne peut évidemment avoir la moindre idée de la date et des conditions de la fin du monde économique, on peut difficilement imaginer qu'elle ne dépasse pas une durée de vie humaine, et rien de sérieux n'est prévisible à de telles échéances. En d'autres termes, la théorie générale est indéfinie vers l'avenir. Donc une condition essentielle à la validité de la théorie concurrentielle n'est pas satisfaite. Il faut alors examiner comment se présente la situation résultante, par rapport à cette théorie. Notre modèle y suffit, les études plus générales le confirment.
VIII - Examen de l'évolution optimale
À l'optimum théorique, les prix et quantités jouissent des propriétés suivantes : les prix étant supposés constants, la somme de leur produit par les quantités est maximale quand les quantités varient en respectant les conditions aux limites et contraintes diverses (fonctions de production etc.). Ceci dérive directement de la définition de l'optimum Pareto (maximum lié, et prix optimaux égaux aux multiplicateurs de Lagrange).
VIII. a - Unicité du taux d'intérêt et du taux d'actualisation
Donnons nous un taux d'intérêt {j} et soit {w=i+j}. Si l'on est bien à l'optimum avec ce taux, la somme des prix actualisés avec lui doit être maximale. On suppose que les choix techniques aient été faits avec le taux {i} avec {u=1+i}. ceci entraîne (§5) :
{} : {x=1/rac (u)} et {y=rac (u)}
Le coût effectivement payé par l'industriel est :
{16} : {x* (w+y)= (w+u)/rac (u)}
La valeur actuelle des productions est celle des dépenses salariales (on vend au coût de revient), mais il faut ajouter la valeur du capital final (N (p) machines correspondant à Q (p+1) et retrancher celle du capital initial. La théorie n'est valable que si ces deux capitaux sont donnés. Quand {w} est ce qu'il est, et que la commande technique d'actualisation varie, ces conditions font que la valeur actualisée en cause varie comme celle des dépenses salariales (on peut le montrer par calcul direct, bien entendu). Cette valeur est :
{17} : {A=No* ( (v^ (p+1)-w^ (p+1))/ (w)* (v-w))}
Les cœfficients des {Q} sont les prix actualisés, savoir
{18} : { (w+u)/rac (u)* (w)}
À cœfficients constants, l'optimum est donc obtenu en maximisant ce terme multiplié par {A}, donc ce terme, puisque {A} ne dépend pas de {u}. En dérivant par rapport à {u}, on trouve {u=w}. Ainsi, il faut donc bien actualiser avec un taux égal au taux d'intérêt si l'on veut obtenir l'optimum Pareto.
Il y a naturellement un os dans le modèle (trop rigide), c'est qu'il n'existe que deux valeurs de {u} donnant le même capital final ; il faut le compliquer en superposant des techniques distinctes pour accroître ces possibilités, et à la limite, pouvoir choisir le capital final. Mais le résultat est le même, car la théorie n'est pas critiquable sur ce point.
VIII. b - Influence du taux sur l'évolution dans le temps
Il nous faut maintenant essayer de comprendre le paradoxe qui se présente quand on ne se fixe pas une limite finie avec des capitaux égaux. Dans le § 6. a, nous avons constaté que le taux d'intérêt influe sur le niveau de vie en permanence, mais dans les systèmes exponentiels permanents, et donc moyennant un capital de départ variable ; on peut se demander si l'écart entre ces niveaux de vie n'est pas simplement la contrepartie d'un écart de valeur en sens contraire pour les capitaux. Mais il suffit, pour le vérifier, de partir d'un état connu caractérisé par un certain outil physique, susceptible de produire {Q (p)} moyennant un appoint de travail précis à l'unité produite. Supposons donc que nous sommes dans le système exponentiel au taux de croissance {a} {1+a=v} et au taux d'actualisation {i} {1+i=u}. On a alors :
{19} Q (p)=Q (o)* (V) avec {Qo=N (o)* (rac (u)/u+v)}
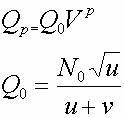
La valeur actuelle des productions {Q}, au taux {i}, comme le coût est {2*rac (u)} est :
{20} : {Q (o)+ƒ[1 :p] (Q (o)*2* (rac (u))*Q (o)* ( (y/u))}
Les autorités décident, l'année zéro, de passer à l'optimum absolu, avec actualisation au taux i=a. Il leur faut passer à :
{21} : {Q (p)=N (o)* (1/2rac (v)*v}
et il suffit pour cela que Q (1) réponde à cette relation, ce qui exige l'année zéro ( (1/2)*No) ouvriers. Or les travailleurs nécessaires à produire Q (o) avec l'ancien type d'investissement (très capitalistique, car {i{a}) sont au nombre de Q (o)*rac (u).
{22} : Q (o)*rac (u)=N (o)* (u/ (u+v))
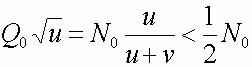
{23} : Il nous reste donc {N (o)* (v/ (u+v))} personnes dont nous utilisons { (1/2)*N (o)} dans l'industrie d'investissement.
Il en reste donc :
{24} : {N (o)* ( (v-u)/ (u+v))=N (o) ( (v/ (u+v)-1/2)}
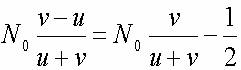
qui pourront fabriquer n'importe quoi en sus de Q (o), ou aller jouer aux boules (congés payés etc.). Supposons qu'on les occupe à fabriquer le même bien aux conditions artisanales du §1. Alors Q (o) est multiplié par :
{25} : {1+ (v-u)/ (2. 2* (u+v))=1+M}
{26} : Tous les Q (p) sont multipliés par { (u+v)/rac (uv)>1}
Donc l'actualisation des {Q}, tous plus élevés que dans le premier cas, donne un total plus élevé avec les mêmes cœfficients, ce qui met en défaut le théorème de base de la théorie. Plus exactement, c'est l'absence d'une condition fixe aux limites du temps qui provoque cette fissure. Il n'en serait plus de même si on décidait de la fin de vie du système par destruction du monde l'année {p}, et si l'on utilisait les hommes disponibles après fabrication des {Q (p)} à des fabrications artisanales, comme nous l'avons fait à {t=0}. Il y a en effet moins de disponibles dans les systèmes {v} que dans les systèmes {u}.
Le recours à des modèles bien plus compliqués ne fait que confirmer ces résultats. Un taux d'actualisation trop bas, c'est-à-dire de forts investissements, conduisent à une perte permanente du niveau de vie par rapport à un autre système moins capitalistique, dont l'obtention comporte un freinage des fabrications d'équipement, un accroissement du taux d'actualisation réel, et une marche de croisière à un taux voisin de celui de progression des salaires.
Si le taux d'actualisation est trop élevé (système sous-capitalistique où notre modèle simplifié est instable, on l'a vu au §6. b), les modèles complexes montrent que ce n'est plus possible, et qu'il faut se serrer la ceinture au début si l'on veut finir par se placer sur la ligne d'évolution optimale permanente ; on ne peut alors qu'arbitrer entre le présent et le futur, et non gagner tout le temps. C'était à prévoir ; d'une part le raisonnement qu'on vient de faire pour l'époque zéro ne marche plus, car il n'y a plus assez d'ouvriers disponibles pour fabriquer l'investissement Q (1) du système {v} quand {v{u} ; d'autre part, le taux d'actualisation excédant la croissance, tous les paramètres physiques tendent vers zéro en valeur actualisée quand {p} tend vers l'infini. Il y a donc un état final à l'infini, avec capital actualisé commun (nul), et le théorème classique redevient valable, on ne peut plus gagner à un moment sans perdre à un autre. Ce qui n'empêche que le critère de maximisation par valeurs actuelles, évident quand il s'agit de l'intérêt financier d'entreprise, est plus que contestable pour l'intérêt général (sauf bien entendu quand les écarts de toutes les époques sont dans le même sens, critère qui est vérifié dans notre petit exemple).
Note sur le progrès technique
S'il y a un progrès au taux {c} -si par exemple {x} diminue à {x/ (1+c)} et {y} à {y/ ( (1+c))} -alors la production {Q} croît comme { (1+c)} et elle est acquise avec un salaire total multiplié par { (1+s)}. Si par exemple le salaire nominal croît au taux {s=c}, le prix du produit reste stable et le salaire "réel" croît toujours comme le salaire nominal. En général (s) est supérieur à {c} ; le salaire réel croît toujours comme la "productivité" (dont le taux de croissance est par définition "{c}"), mais le salaire nominal croît plus vite : s}c. Il y a inflation des prix et salaires, ce qu'on appelle aussi dévalorisation monétaire. Les lignes qui précèdent supposent apparemment que la population est stable, mais on constate facilement que rien n'est à modifier si elle se modifie (taux "{a}" des données).